This unit is all about infinite series, or the summation of a sequence with an infinite number of terms. That is, if {a_n} is an infinite sequence, then the infinite series would be the following:
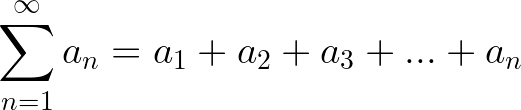
But what does any of that mean? Let’s break it down.
Sequence
A sequence is a list of numbers in a certain order. Each number in a sequence is called a term. Each term has a position denoted by the subscript (little number on the bottom). You can find the nth term of a sequence by plugging in for n.
Partial Sum
A series is the sum of the terms of a sequence. We use big Sigma (∑) notation to let us know that each term is being added (usually either n = 0 or n = 1). The lower bound lets us know at which a_n to start adding. The upper bound lets us know where to stop adding.
Series
A series in AP Calc is just a sum that goes to infinity! In other words, you continue adding each term forever to get the sum.
Definition of Convergent & Divergent Series
Let’s imagine you have a big bag of marbles. Now, if every time you add a new marble (nth term), the total number of marbles (nth partial sum) gets closer and closer to a certain number, that’s like a convergent series. It’s like when you’re counting and you keep getting closer to a final number.
But if every time you add another marble (nth term), the total number of marbles (nth partial sum) just keeps getting bigger and bigger, without ever getting close to a final number, that’s like a divergent series. The number of marbles (nth partial sum) keeps getting bigger and bigger without ever converging to a final sum.
Properties of Infinite Series
